广义相对论的数学基础（十五）：联络

联络

对于一个给定的光滑流形，我们如何描述它是“平坦”的或还是“弯曲”的？

直观地，我们认为三维空间中的一个平面是“平坦”的，而一个二维的球面是弯曲的。这种描述不仅仅是依赖于流形的非内禀结构（将它们嵌入到高维的流形），而且这个这些所谓的“平坦”或“弯曲”也是非内禀的。

事实上这里的弯曲和平坦对应于我们以后将要讨论的子流形的外曲率。它描述的是 子流形如何嵌入在高维流形，而非这个子流形 内禀的弯曲程度。

若希望得到内禀的弯曲程度，我们须将自己想象成被限制在这些流形上的生物。这样的生物能否够感知到它所在流形的弯曲程度？而又如何才能感知到这种弯曲程度？

一个简单的想法：
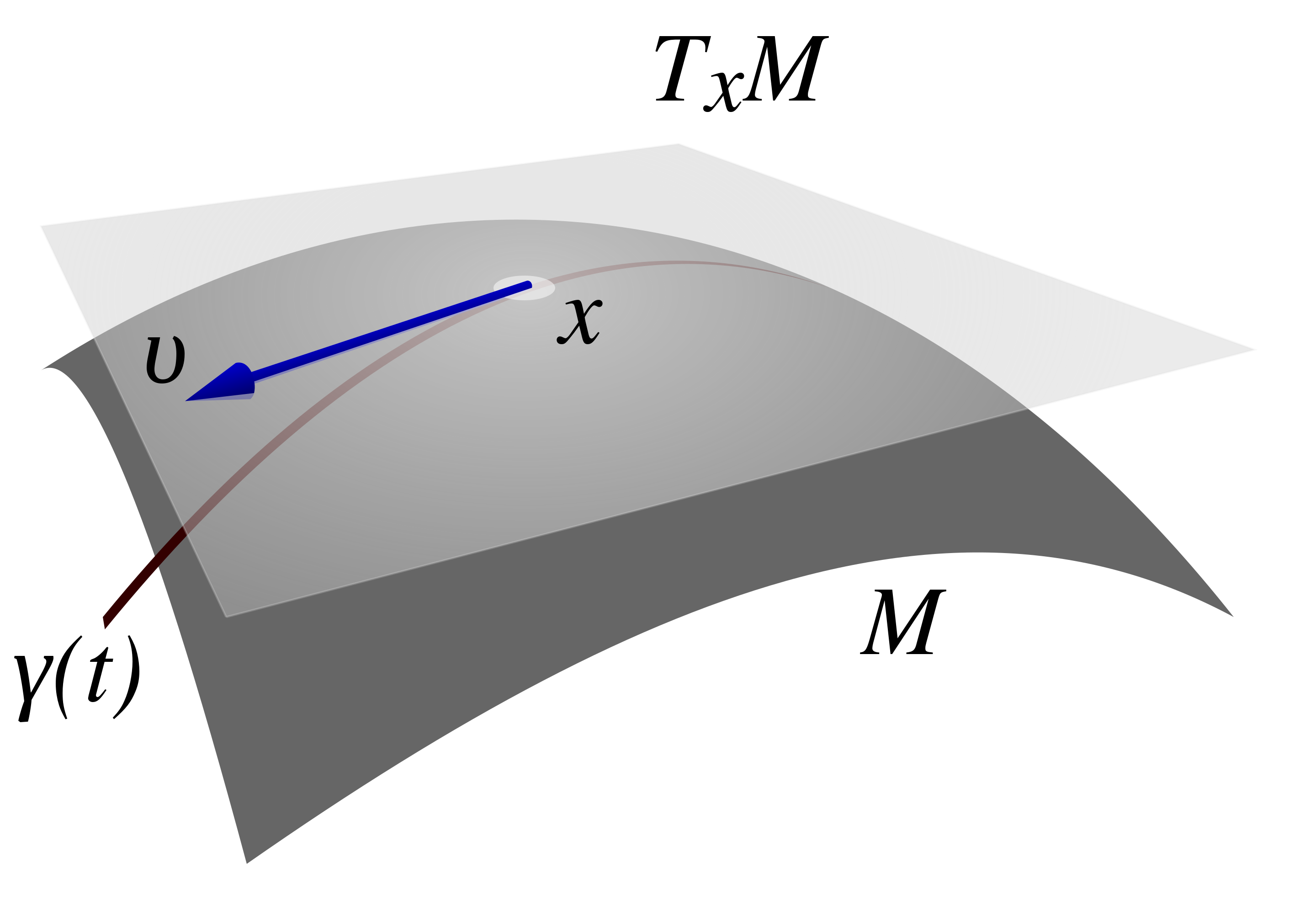
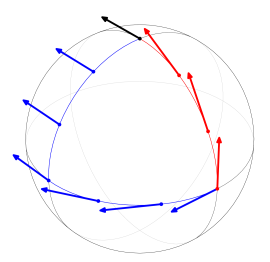
使用平行移动一个箭头的办法来确定我们所处的地球是弯曲还是平坦的。

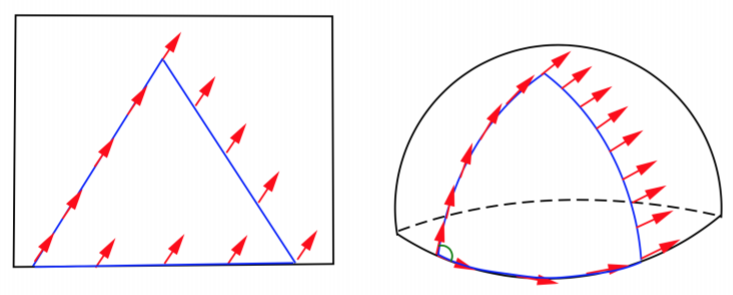
Fig：平行移动示意图

对于一个给定的光滑流形，我们可以在它的每一点上建立一个线性空间，即切空间。一点处的两个切矢量是可以谈平行的概念的。但两个不同点处的切矢量之间是不能谈平行与否的，因为它们分别属于不同的线性空间。因此在光滑流形上我们暂时还没有沿着某条曲线平行移动的概念。

为了建立平行移动的概念，我们必须要在两点的切空间之间建立某种联系，这种联系就是所谓的联络。对于光滑流形上的两点（不一定临近，但可通过曲线相连），我们可以建立它们相应切空间之间满足某种要求的同构，光滑流形上所有这些同构形成的系统便可以定义为联络。事实上这样定义的联络可以建立两点处切空间之间的平移同构。

继续二维生物的思考。沿着某条曲线，要求相邻的箭头尽可能的“平行”。这意味着“箭头”沿着曲线的切矢量的某种变化要满足一定的条件，这是一种“箭头”沿着曲线切矢量微商或求导的概念，对应于联络一种无穷小的形式。

这种无穷小形式也是定义联络时最容易接受的一种形式。特别地，对于平面的情况，若将“箭头”看成是切矢量，“平行移动”意味着这个切矢量沿着曲线的切矢量的“方向导数”为零。因此我们自然地想到: 对于一般曲面的情况，是否可以定义某种推广的方向导数，使得平行的概念也有类似的定义？如果我们能够得到了这种类似的“方向导数”，则可定义平行移动，从而给出了某个联络结构的无穷小实现。

那么李导数是否满足上述要求呢？在局部坐标下有：

$(\mathcal{L}_vu)^i = v^j\partial_ju^i - u^j\partial_j v^i$

其中包含了 $v$ 的变化，这与“方向导数”的概念是不相符的（方向都变了，自然谈不上什么方向导数）。因此我们要定义一个新的导数概念。

联络是光滑流形的微分结构之外的一种新的数学结构。有了它之后，我们便可以在流形上谈论平行移动的概念。

按前面所述，比较方便的做法是引入某种推广的方向导数，即下面将要引入的协变导数或协变微商的概念。有了联络之后，我们便可以定义平行移动。进一步地，还可以通过这种联络结构来描述流形的弯曲程度，也就是所谓流形的曲率。

协变微商

协变微商 (covariant derivative or absolute derivative)
设 $X$ 是 $n$ -维光滑流形，（仿射）联络 $\nabla$ 是一个映射，它将一个切矢量映为一个 $(1,1)$ -型张量场，并满足

$\nabla(u + v) =\nabla u + \nabla v$
$\nabla (fv) = df \otimes v + f\nabla v$

其中 $v ,u$ 是两个切矢量，而 $f\in\mathscr{F}(X)$ 。 $\nabla u$ 称为 $u$ 的协变微商、协变导数、或绝对微商 (covariant derivative or absolute derivative)。

参照陈省身的讲义第四章，我们可以用矢量丛的语言定义联络。可以将上面的联络可以理解为一个映射：

$\nabla : \Gamma(TX) \rightarrow \Gamma(T^* X \otimes TX)$

粗略地说，流形 $X$ 的切丛 $TX$ 是一个集合

$TX =\bigcup_ {p\in X}T_p X$

并赋予光滑结构，使之成为一个 $2n$ 维的光滑流形。 $\Gamma(TX)$ 是切丛截面的集合，它形成一个无穷维的线性空间，也是 $F(X)$ 上的模。每一个截面称为一个切矢量场，并可证明

$\Gamma(TX) = \mathscr{X} (X)$

$T^*X$ 是 $TX$ 的对偶丛，可将其看成是 $\bigcup_{p\in X} T^*_pX$ 形成的集合并赋予了光滑结构。 $T^*X$ 的截面是对偶矢量场或 $1$ -形式场。
而 $TX \otimes T^* X$ 称为切丛 $TX$ 和其对偶丛 $T^* X$ 的张量丛，其截面是流形 $X$ 上的光滑 $(1,1)$ -型张量场。
用丛的语言来说，我们考虑的是切丛上的联络。按照习惯上，切丛 $TX$ 上的联络称为流形 $X$ 上的仿射联络（有时候也称为线性联络。线性联络和仿射联络往往可以混用，它们的区别和联系见 Kobayashi 的书）。

沿着切矢量场的协变导数
设 $u$ 是一个切矢量场，因 $\nabla v$ 是一个 $(1,1)$ -型张量，因此可定义：

$\nabla _ u v = \nabla v(u)$

因 $\nabla_v$ 是 $(1,1)$ -型张量，它作用在切矢量场 $u$ 后仍然得到一个切矢量场。从而 $\nabla_u$ 将一个切矢量场映成一个切矢量场，由定义很容易看出 $\nabla_u v$ 关于 $u$ 是 $\mathscr{F}(X)$ -线性的，即我们有：

$\nabla_ {fu+gw} v = f\nabla_ u v + g\nabla_ w v$

$\nabla_ u v$ 称为切矢量场 $v$ 沿着切矢量场 $u$ 的 协变导数 或 协变微商。

局部坐标下的表述
设 $u = u^i \frac{\partial}{\partial x^i}, v = v^i \frac{\partial}{\partial x^i}$ ， $u^i$ 和 $v^i$ 都是坐标域上的光滑函数。则我们有：

$\nabla v=\nabla (v^i\frac{\partial}{\partial x^i})=dv^i\otimes\frac{\partial}{\partial x^i}+v^i\nabla\frac{\partial}{\partial x^i}$

因 $\nabla(\frac{\partial}{\partial x_ i} )$ 是一个 $(1,1)$ -型张量，因此局部上可以表示为：

$\nabla\frac{\partial}{\partial x^i}=\Gamma^k_{\ \ ji}dx^j\otimes\frac{\partial}{\partial x^k}=\omega^k_{\ \ i}\otimes \frac{\partial}{\partial x^k}$

其中 $\Gamma^k_{\ \ ji}dx^j$ 是一组光滑函数，称为 联络系数 或者 Christoffel 符号。而

$\omega^k_ {\ \ i} = \Gamma^k_{\ \ ji}dx^j$

称为 联络 $1$ -形式。

这样，我们便得到

$\nabla v=(\frac{\partial v^k}{\partial x^j}+\Gamma^k_{\ \ ji}v^i)dx^j\otimes\frac{\partial}{\partial x^k}$

或者

$\nabla v=(dv^i+\omega^i_{\ \ j}v^j)\otimes\frac{\partial}{\partial x^k}$

可进一步得到

$\begin{aligned} \nabla_u v &= \nabla v(u) = (\frac{\partial v^k}{\partial x^j}+\Gamma^k_{\ \ ji}v^i)dx^j\otimes\frac{\partial}{\partial x^k}(u^l\frac{\partial}{\partial x^l})\\ &= u^j(\frac{\partial v^k}{\partial x^j}+\Gamma^k_{\ \ ji}v^i)\frac{\partial}{\partial x^k}\\ \end{aligned}\tag{1}$

特别地，我们有

$\nabla_{\frac{\partial}{\partial x^j}}\frac{\partial}{\partial x^i}=\Gamma^k_{\ \ ji}\frac{\partial}{\partial x^k}$

为了方便，引入记号 $\nabla_i=\nabla_{\frac{\partial}{\partial x^i}}$ ，有：

$\nabla_{j}\frac{\partial}{\partial x^i}=\Gamma^k_{\ \ ji}\frac{\partial}{\partial x^k}$

由方程 $(1)$ 容易看出： $v$ 沿着 $u$ 的协变微商或协变导数并不改变 $u$ 的 “方向”，即和 $u$ 的分量的变化没有关系，因此一个切矢量场沿着另外一个切矢量场的“方向导数”的概念就有了。

平行移动

平行移动 (Parallel transport of vector )
设 $v(t)$ 是定义在曲线 $c : I \rightarrow X ,t \mapsto c(t)$ 上的切矢量。我们称 $v(t)$ 沿着曲线 $c$ 是平行移动的，若：

$\nabla_ u v = 0$

其中 $u$ 是这条曲线的切矢量。在局部坐标下， $u,v$ 可以表示为：

$\begin{aligned} &u(t) = u^i(t)\frac{\partial}{\partial x^i} = \frac{dx^i(c(t))}{dt}\frac{\partial}{\partial x^i} = \frac{d(c(t))^i}{dt}\frac{\partial}{\partial x^i}\\ &v(t) = v^i(t)\frac{\partial}{\partial x^i} = v^i(c(t))\frac{\partial}{\partial x^i}\\ \end{aligned}$

因此平行移动意味着：

$\frac{dx^i(c(t))}{dt}\frac{\partial v^k}{\partial x^j} + \Gamma^k_{\ \ ji}v^i\frac{dx^j(c(t))}{dt} = 0$

或者简写为：

$\frac{dv^k(t)}{dt}+\Gamma^k_{\ \ ji}u^j(t)v^i(t)=0$

这就是平行移动的分量表述。

测地线

仿射测地
曲线 $c : I \rightarrow X ,t \mapsto c(t)$ ，如果满足

$\nabla_ u u = \lambda u$

称为是 仿射测地 (affine geodesic) 的。其中 $u$ 是曲线的切矢，而 $\lambda$ 是 $I$ 上的函数，即 $\lambda : t \mapsto \lambda(t)$ 。

测地
如果曲线 $c$ 满足

$\nabla_ u u = 0$

则称其为 测地 (geodesic) 的。

容易看出在局部坐标下，此方程可表示为：

$\frac{d^2 x^k}{dt^2}+\Gamma^k_{\ \ ji}\frac{dx^j}{dt}\frac{dx^i}{dt}=0$

若一条曲线是仿射测地的，则我们总可以通过重新选取曲线参数 $t$ ，将其变成测地曲线。

Koszul 联络

Koszul 在 1950 年代提出如下联络的定义，现在被广泛使用。

Koszul 联络
设 $u,v,w \in \Gamma(TX),\ f \in \mathscr{F}(X)$ 。联络 $\nabla$ 是一个映射：

$\nabla : \Gamma(TX)\times \Gamma(TX) \rightarrow \Gamma(TX)$

满足

$\nabla_u (v + w) = \nabla_ u v + \nabla_ u w$
$\nabla_{fu} v = f\nabla_ u v$
$\nabla_{u+v} w = \nabla_ u w + \nabla_ v w$
$\nabla_ u (fv) = u(f)v + f\nabla_ u v$

事实上，这个定义中的四条可以看成是上一节协变微商定义的推论。

联络的推广

我们现在想把联络进行推广到一般的张量上。这可以从协变微商与 Koszul 联络两个角度出发。

协变微商的推广

首先对于光滑函数 $f\in\mathscr{F}(X)$ ，我们可以定义 $\nabla f =df$ 。若将协变微商推广到一般张量，我们也期望 Leibniz 法则也能够适用。
其次，设 $v$ 是一个矢量场，而 $\theta$ 是一个对偶矢量场，则 $\theta(v) = \langle v, \theta\rangle = C(v\otimes \theta)$ 是一个光滑函数。我们可以将 $\nabla$ 扩张到对偶矢量场 $\theta$ ，使得下面表达式成立：

$\langle \nabla v,\theta\rangle + \langle v,\nabla\theta\rangle = \nabla\langle v,\theta\rangle = d\langle v,\theta\rangle$

从而可以得到：

$\begin{aligned} d\langle v,\theta\rangle &= d\circ C(v\otimes \theta)\\ &= \nabla \circ C(v\otimes \theta)\\ \end{aligned}$

另一方面：

$\begin{aligned} \langle \nabla v,\theta\rangle + \langle v,\nabla\theta\rangle &= C(\nabla v\otimes \theta + v\otimes \nabla \theta)\\ &= C \circ \nabla (v\otimes \theta) \end{aligned}$

即要求 $\nabla$ 与缩并运算 $C$ 可交换。

这样我们可以得到 一般张量的协变微商的定义：
$\nabla$ 是一个映射，它将 $(r,s)$ -型张量场映为 $(r,s + 1)$ -型张量场，并满足：

$\nabla(\tau + \sigma) = \nabla\tau + \nabla\sigma$
$\nabla f = df$
$\nabla(\tau \otimes \phi) = \nabla\tau \otimes \phi + \tau \otimes \nabla\phi$
$\nabla \circ C = C \circ \nabla$

其中 $f$ 是光滑函数， $\tau,\sigma$ 是两个类型相同的张量场，而 $\phi$ 是另一个任意类型的张量场。符号 $C$ 代表某个缩并算子。

进行一些特别考虑。设 $\{e_i\}$ 与 $\{e^{*i}\}$ 分别是某个局部基和对偶基。则有：

$\langle \nabla e_i,e^{*j}\rangle + \langle e_i,\nabla e^{*j}\rangle = d\langle e_i,e^{*j}\rangle = 0$

通常我们能找到一个联络 $1$ -形式，将 $\nabla e_i$ 展开为：

$\nabla e_i = \omega^j_{\ \ i} \otimes e_j$

如此得到：

$\langle \omega^k_{\ \ i} \otimes e_k,e^{*j}\rangle + \langle e_i,\nabla e^{*j}\rangle = 0$

最终结果为：

$\langle e_i,\nabla e^{*j}\rangle = -\omega^j_{\ \ i}$

设 $\nabla e^{*j} = \omega^{*j}_{\ \ \ \ k}\otimes e^{*k}$ ，其中 $\omega^{*j}_{\ \ \ \ k}$ 是一些 $1$ -形式场，则有：

$\langle e_i,\omega^{*j}_{\ \ \ \ k}\otimes e^{*k}\rangle = \omega^{*j}_{\ \ \ \ i} = -\omega^j_{\ \ i}$

那么一个余切矢量的协变微分可以写为：

$\nabla \theta = \nabla(\theta_ie^{*i}) = (d\theta_i - \omega^j_{\ \ i}\theta_j)\otimes e^{*i}$

Koszul 联络的推广

一般张量场的 Koszul 协变微商
类似地，我们也可以将沿着某个切矢量场 $u$ 的 Koszul 协变微商 $\nabla_u$ 推广到一般张量，它将 $(r,s)$ -型张量场映为 $(r,s)$ -型张量场，并满足：

$\nabla_ u (\tau + \sigma) = \nabla_ u \tau + \nabla_u\sigma$
$\nabla_ {fu} \tau = f\nabla_ u \tau$
$\nabla_ {u+v} \tau = \nabla_ u \tau + \nabla_ v \tau$
$\nabla_ u (\tau \otimes \phi) = \nabla_ u \tau \otimes \phi + \tau \otimes \nabla_ u \phi$
$\nabla_ u f = u(f) = \mathcal{L}_ u f$
$\nabla_ u \circ C = C \circ \nabla_ u$