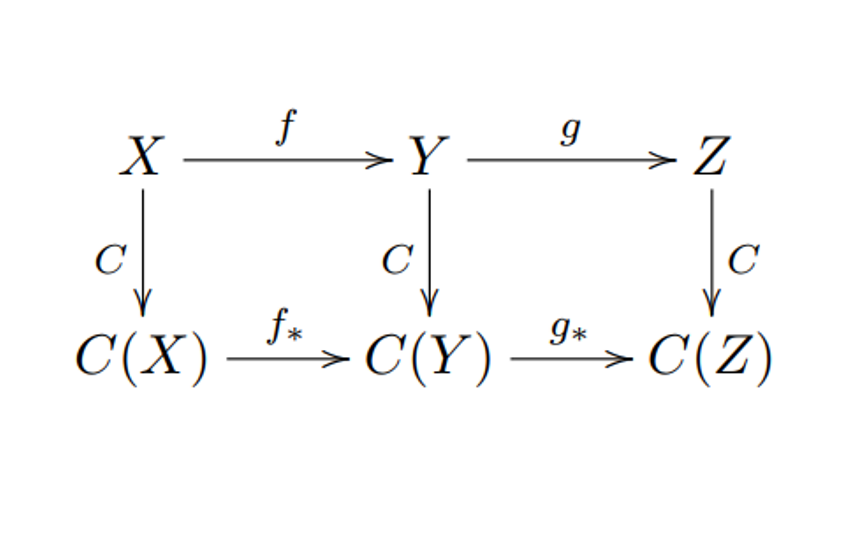拓扑流形
流形 (manifold)
设 X 是一个 Hausdorff 拓扑空间,∀p∈X,都有 p 的一个邻域 N(p) 同胚于 Rn 中的某个开集。则称 X 为一个 n-维的拓扑流形(或简称流形)。
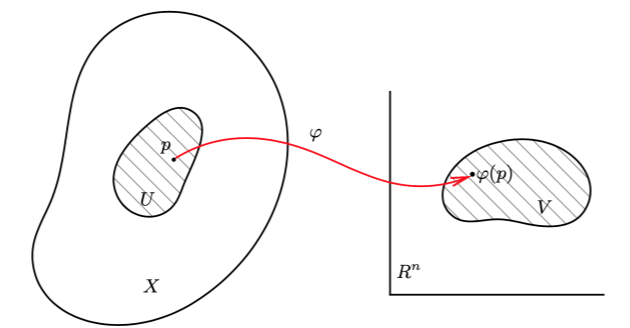
流形局部像欧式空间
坐标卡 (chart)
流形 X 上的坐标卡是一个二元组 (U,φ),其中 U 是 X 的开集,称为坐标卡的定义域;φ 是一个从 U 到 Rn 上某个开集 V 的同胚:φ:U→V。有时也称其为局部坐标系。
设 p∈U,则 φ(p)∈V⊂Rn 。在 Rn 中 φ(p) 可以用一组数
(x1(p),⋯,xn(p))
表示。这组数称为点 p 在坐标卡 (U,φ) 中的坐标 (coordinates)。有时候,人们称 xi 是坐标函数。它们是 Rn 上的一组映射:
xi:Rn→Ru↦xi(u)=(u)i, ∀u∈Rn
坐标函数 xi 的作用是:对 Rn 中的任意一点 u,给出它的第 i 个坐标 (u)i。xi(p) 是 xi∘φ(p) 的简写。比较细致地,我们可以定义复合映射:
xφi=xi∘φ:p↦xφi(p)=(φ(p))i
对于每一个 p,给出它在坐标卡 (U,φ) 下的坐标 xφi(p)(或 xUi(p))。用下标 φ (或 U) 可以明确的指出 xφi (或 xUi)是坐标卡 (U,φ) 下的坐标函数。xφi 的作用是:对于每一个 p,给出它在坐标卡 (U,φ) 下的坐标
微分流形
坐标卡集与微分结构
流形 X 上的 Ck 类 坐标卡集 (altas) 是流形 X 上的坐标卡的集合 {(Uα,φα)},并要求这些坐标卡满足下面条件:
- {Uα} 是 X 的一个覆盖
- 相容性条件
由同胚 φα 给出的映射
φβ∘φα−1:φα(Uα∩Uβ)→φβ(Uα∩Uβ)
是 Rn 中开集与开集间的 Ck 类(同胚)映射,即:
xi↦yi=yi(x1,⋯,xn)
是 n 个 Ck 类函数。这时,我们称这两个坐标卡是 Ck-相容的。
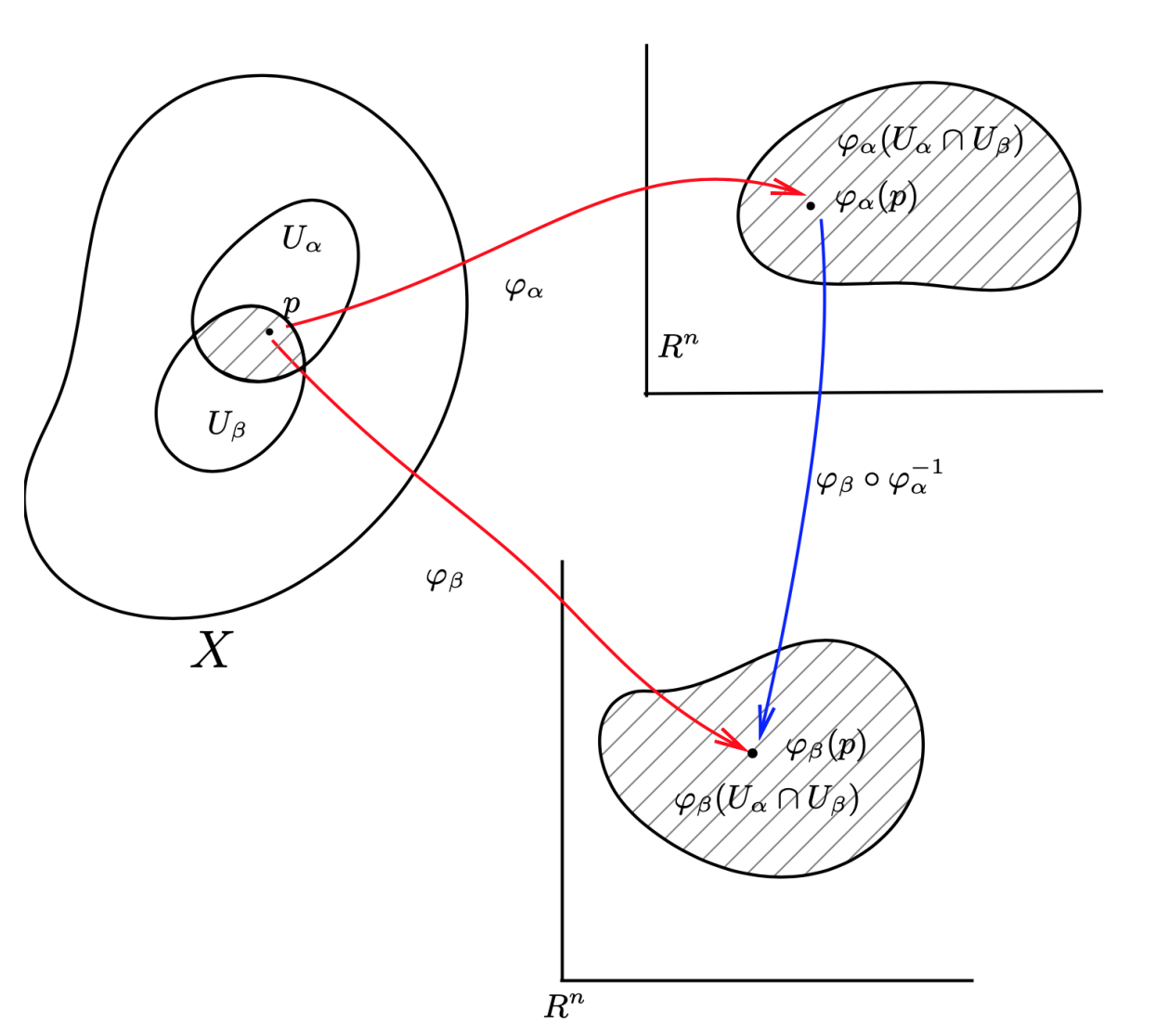
两个 Ck 类坐标卡集称为是等价的,若它们的合并还是一个 Ck 类的坐标卡集。即:{Uα,Uα′} 形成一个新的坐标卡定义域,而 {ϕα,ϕα′} 是相应的同胚。并要求这个新的坐标卡集也是 Ck 类的。利用这种等价关系可以给出 微分结构 的概念。按上述等价关系,可以得到所有 Ck 类坐标卡集的等价类。而这个等价类便称为一个 Ck 类微分结构。
例:
极大坐标卡集
设 X 是一个 n− 维流形,A={(Uα,φα)} 是它的一个坐标卡集,并满足下面条件:
- {Uα} 是 X 的一个开覆盖;
- A 中的任意两个坐标卡是 Ck-相容的;
- A 是极大的,即若 (U,φ) 是 X 的任一个坐标卡且和 A 中每个坐标卡都是 Ck-相容,那么它必然属于 A。
极大坐标集构成一个微分结构。
微分流形
对于拓扑流形 X,赋予其一个 Ck 类微分结构,便称为一个 Ck 类 微分流形。若要求对考虑的问题,k 足够大 (以后我们遇到的通常是这种情况),即 C∞ 类微分流形,又被称为 光滑流形。
一个拓扑流形可以赋予不同的微分结构,得到不同的微分流形。实微分流形是在局部上以 Rn 为模板得到的不同微分流形。
实解析流形 (real analytic)
也记为 Cω 类微分流形. 要求函数 φβ∘ϕα−1 是实解析的.
复解析流形 (real analytic)
要求函数 φβ∘φα−1 是全纯的 (holomorphic)或复解析的。
直积流形
我们可以从拓扑流形 Xn 与 Ym 上出发构造直积流形。设它们的拓扑分别为 UX 和 UY,我们可以赋予直积流形 Zn+m=Xn×Ym 乘积拓扑。
对于拓扑流形 Xn 与 Ym,我们可以分别在其上引入微分结构及其相应的坐标卡集 {(UX,φX)} 和 {(UY,φY)},这样 Xn 和 Ym 成为两个微分流形。
由坐标卡集 {(UX,φX)} 和 {(UY,φY)},我们可以构造 Zn+m 的坐标卡集 (UZ,φZ):该坐标卡的定义域为 UZ=UX×UY,而相应的映射 φZ 定义为:
φZ(p,q)=(φX(p),φY(q)),∀ (p,q)∈UZ
这样 Zn+m 上便有了一个微分结构,这样构造出来的微分流形 Zn+m 称为 Xn 和 Ym 的直积流形。
可微映射
可微函数
可微函数 (differentiable)
微分流形上的函数 f 在点 p 称为是可微的,如果在点 p 的某个坐标卡 (U,φ),函数
F=f∘φ−1
在 φ(p) 是可微的。
这个定义不依赖于坐标卡的选取:若 f∘φ−1 在 φ(p) 可微,则在 p 的任意一个坐标卡 (U~,φ~) 在 φ~(p) 也是可微的,这是由于:
f∘φ~−1=(f∘φ−1)∘(φ∘φ~−1)
也是可微的。
r 阶可微函数
函数 f 称为是 Ck 微分流形上点 p 处的 Cr 函数 (r⩽k),如果在 p 的某个坐标卡 (U,φ),f∘φ−1 在 φ(p) 是 Cr 的。
因 φ∘φ~−1 是 Ck 的,所以若想得到坐标卡不依赖的定义,我们要求 r⩽k。
Cr 类函数
微分流形 X 上的函数 f:X→R 称为是 Cr 的,如果它在 X 上的每一点都是 Cr 的。微分流形 X 上的所有 Cr 函数的集合,记为 Fr(X)。
可微映射
流形间的映射
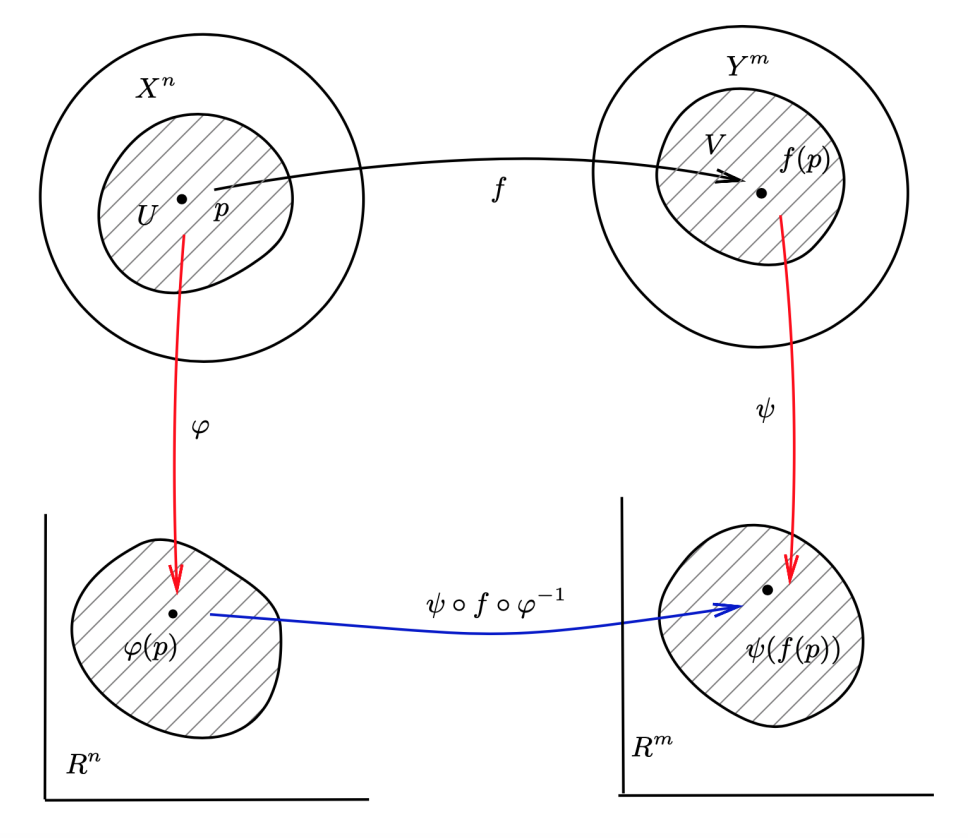
设 Xn 和 Ym 是两个 Ck 微分流形,f 是一个映射:f:Xn→Ym。设 (U,φ) 是 Xn 的一个坐标卡,而 (V,ψ) 是 Yn 的一个坐标卡,则映射 F:
F=ψ∘f∘φ−1
这是一个由 Rn 中的开集到 Rm 中开集的映射。
流形间的映射 f 称为在点 p∈Xn 称为是 Cr 可微的 (r⩽k),若映射 F=ψ∘f∘φ−1 在 φ(p) 是 Cr 可微的,即:
yI=FI(x1,⋯,xn),I=1,⋯,m
是 m 个 Cr 个可微函数,其中 {xi,i=1,⋯,n} 是点 p 的坐标,而 yI,I=1,⋯,m 是点 f(p) 的坐标。
其中条件 r⩽k 保证这个可微的定义不依赖于坐标卡的选择。
若映射 f:Xn→Ym 在点 Xn 的每一点都是 Cr 可微的,则称 f 是 Xn 到 Ym 的 Cr 可微映射。
一些例子:
- 若取 Ym 为 R,得到了我们前面有关可微函数的定义。
- 若取 Xn 为 R 中的一个区间 I,则我们得到了 Ym 上的 Cr 类参数曲线。
曲线
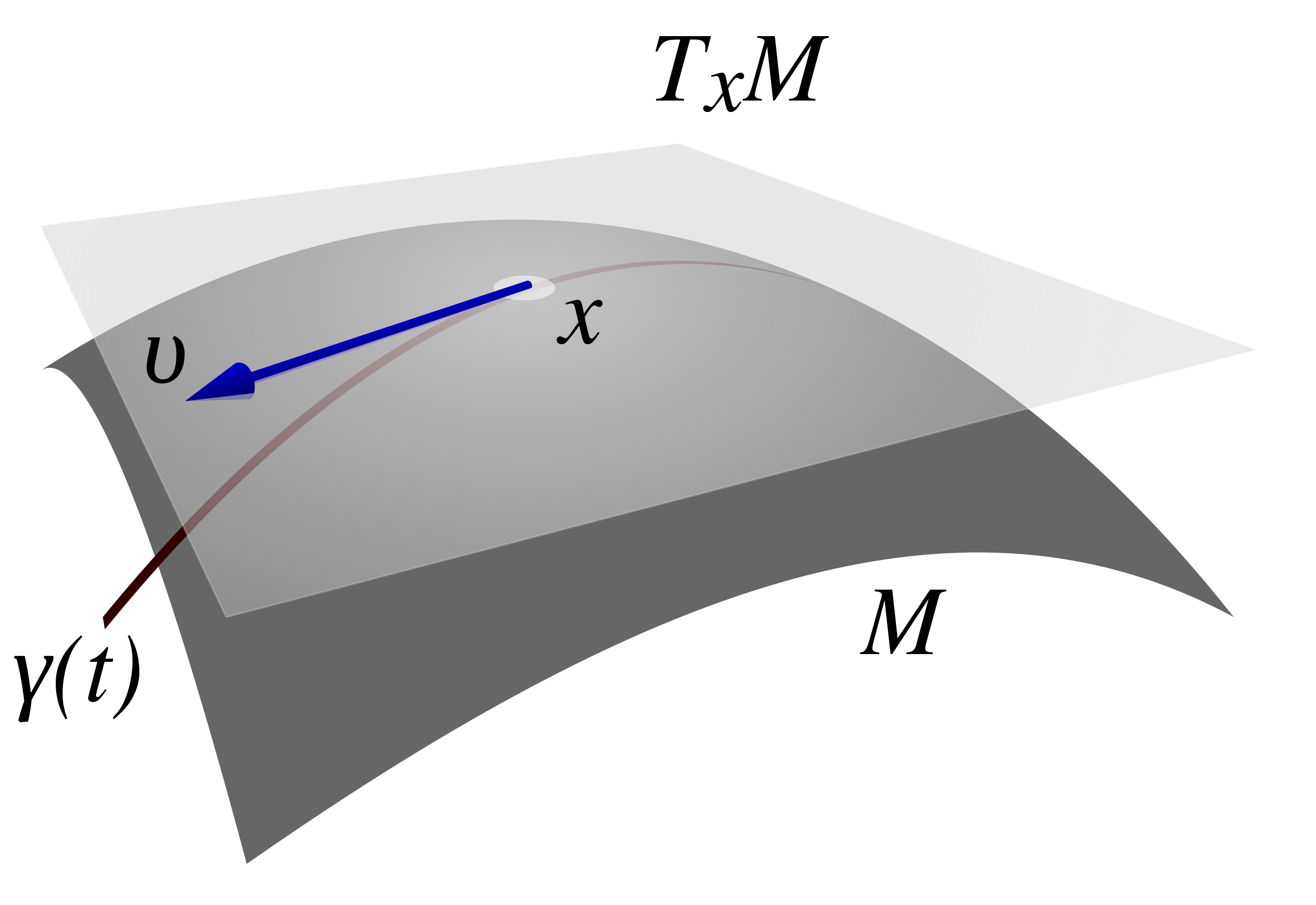
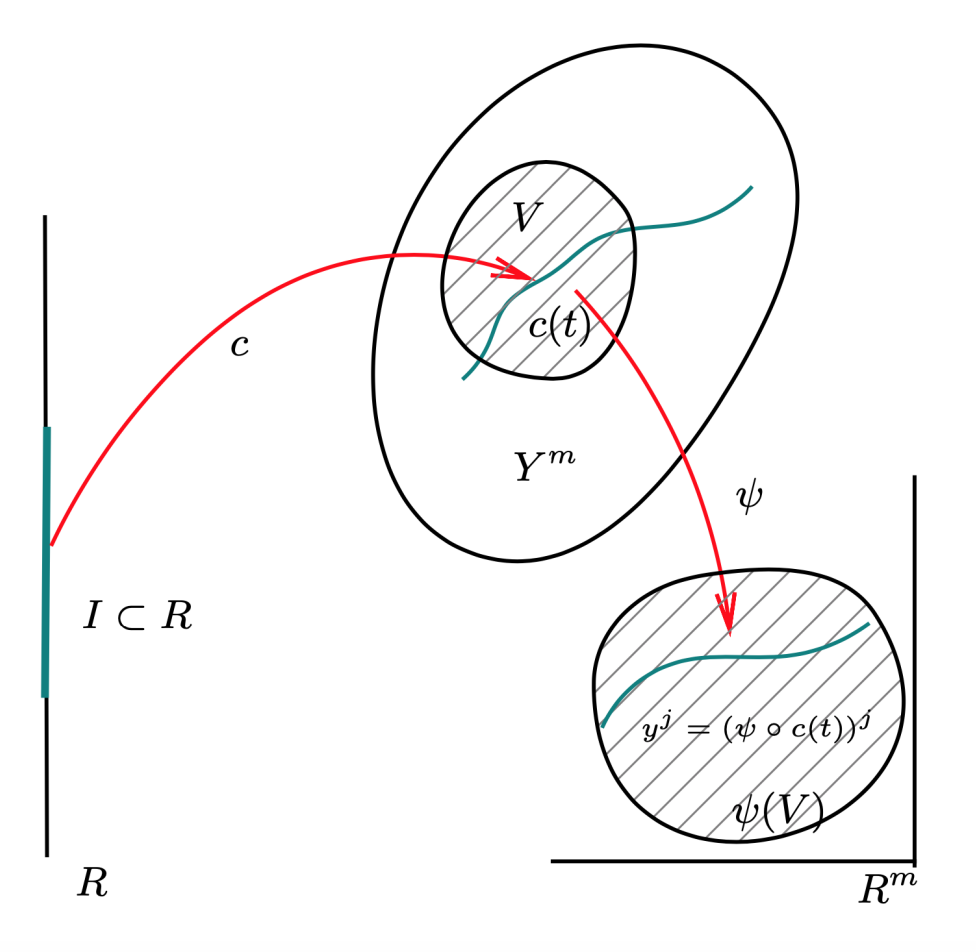
设 X 是一个 n-维微分流形,映射 c:I→X,t↦c(t) 称为 X 的一条曲线。在 X 的坐标卡 (U,φ) 下,该曲线可表示为:
xi=(φ ∘ c(t))i,i=1,⋯,n
其中 xi 是这个坐标卡下的坐标。在不引起歧义时,我们也将上面的表达式简写为:
xi=ci(t) or xi=xi(t)
微分同胚 (diffeomorphism)
设 Xn 和 Yn是 Ck 微分流形。若存在一个映射 f:X→Y 满足:
- f 是双射
- f 和 f−1 都是 Cr 可微的
则称 Xn 和 Yn 互为 Cr 微分同胚。映射 f 称为是一个 Cr 微分同胚映射,或简称 Cr 微分同胚。
若两个微分结构是微分同胚的,则它们具有相同的微分结构(Cr 微分结构)。但是需要指出,两个同胚的流形不一定是微分同胚的(可能微分结构不一样)。
现在,若无特殊说明,我们假定考虑的微分流形都是光滑的,即 k 足够大。所有光滑流形(对象),以及它们之间的光滑映射(态射)形成一个范畴。微分同胚对应于同构态射。
光滑函数的线性空间
光滑流形 X 上的所有光滑函数的集合 F∞(X) 形成一个 R 上的线性空间,可以简记为 F(X)。加法和数乘定义为
(f1+f2)(p)=f1(p)+f2(p),(λf)(p)=λf(p)∀f1,f2∈F(X), ∀p∈X, ∀λ∈R
光滑函数环
事实上,我们还可以在这个线性空间 F(X) 中定义一个乘法:
(f1f2)(p)=f1(p)f2(p)
使得 F(X) 在这样的加法和乘法下成为一个环。当然它也是实数域 R 上的一个代数。
光滑函数的拖回映射 (pull back)
在微分几何中,拖回是将一个流形上某种结构转移到另一个流形上的一种方法。
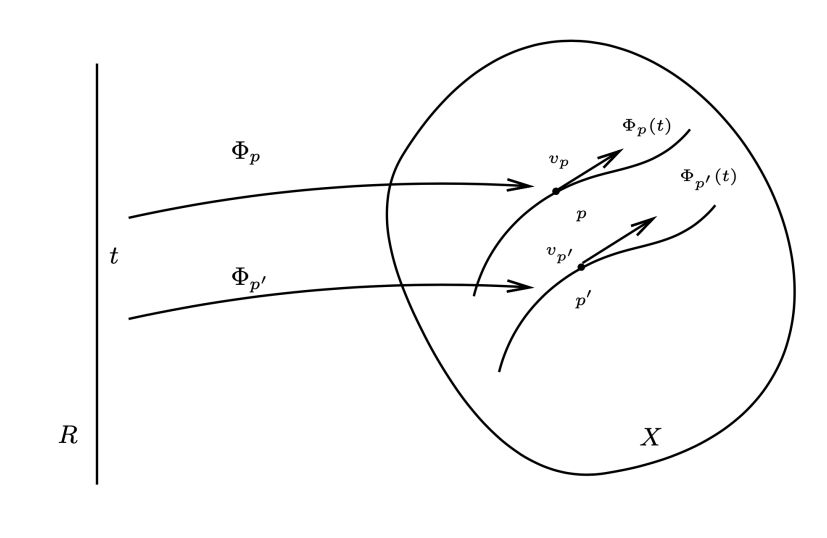
设 Φ:X→Y 是一个光滑映射。则映射 Φ 诱导出 F(Y) 到 F(X) 的映射 Φ∗ 。若 g∈F(Y),Φ∗g 定义为 (映射的复合):
(Φ∗g)(p)=g(Φ(p))=g∘Φ(p)
上面关于映射拖回的定义实质上给出了一个由“微分流形和可微映射形成的范畴”到“线性空间和线性映射形成的范畴”的逆变函子。
微分结构和群结构
前面讲到,引入拓扑结构之后,我们可以得到所谓的拓扑群或连续群. 现在除了拓扑结构,我们又有了微分结构。可以预想的,我们会得到一些关于群的可微的概念。在拓扑群上引入与群运算相容的微分结构后,我们便得到所谓的 Lie 群。
李群 (Lie group)
李群 G 是一个群,同时又是一个微分流形。其上的微分结构和群结构是相容的,即要求群操作:
G×G→G,(x,y)↦xy−1
是可微映射 (光滑映射)。
李群同构 (isomorphic)
两个李群称为是同构的,如果他们之间存在一个保持群结构(群同态)的微分同胚。
例如一般线性群 GL(n,R),容易在上建立坐标卡,使之成为一个微分流形。