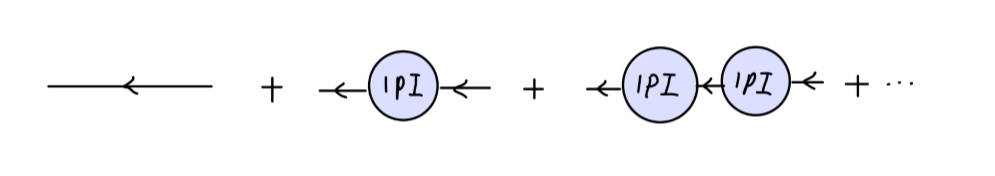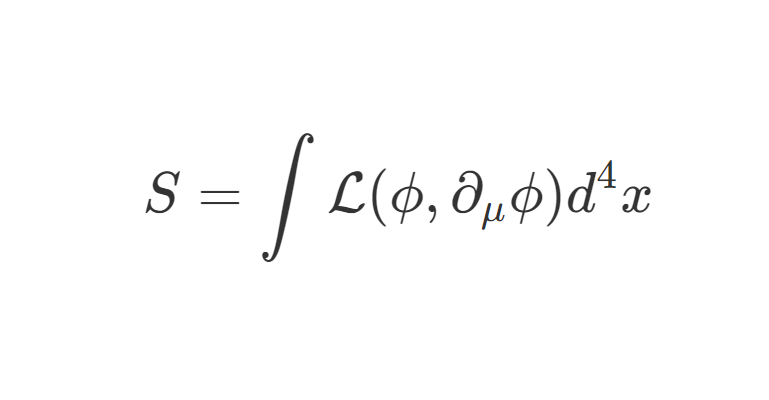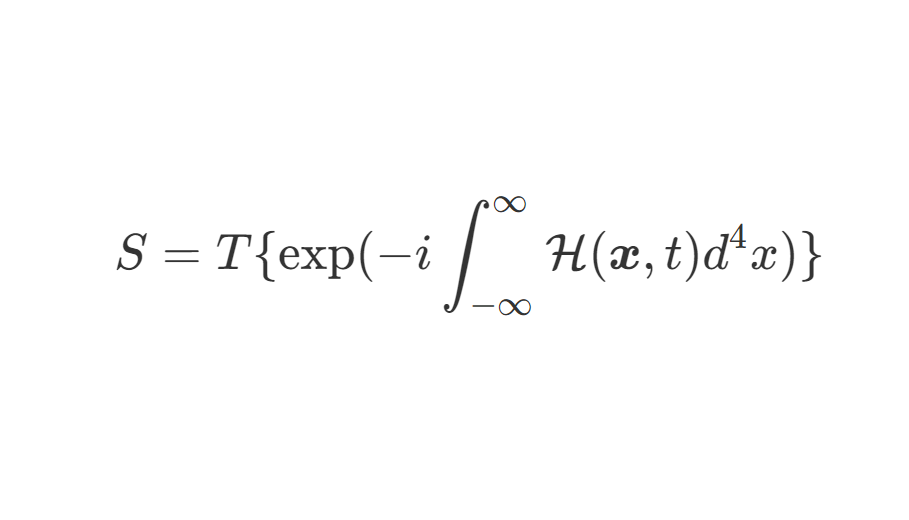场强重整化
两点关联函数的结构
我们现在来研究如下两点关联函数的解析性质。
⟨Ω∣Tϕ(x)ϕ(y)∣Ω⟩
对于自由场的两点关联函数来说,有:
⟨0∣Tϕ(x)ϕ(y)∣0⟩=DF(x−y)=∫(2π)4d4pp2−m2+iϵie−ip(x−y)
p2=m2 为该传播子的极点,对应一个质量为 m 的自由粒子态。
为了观察一般的两点关联函数,我们首先在两个场量间插入一个恒等算子。常用的技巧,我们利用完备性写出恒等算子。
对于单粒子态来说,有:
(1)1−particle=∫(2π)3d3p2Ep1∣p⟩⟨p∣
现在我们做一些推广。对于一个哈密顿量 H 的零动量本征态 ∣λ0⟩ 有 P^∣λ0⟩=0。那么对 ∣λ0⟩ 态的所有 boost 实际上也是哈密顿量的本征态。我们定义 ∣λp⟩ 为 ∣λ0⟩ 经过 boost 后得到的动量为 p 的态。其能量为:Ep≡∣p∣2+mλ2。那么,我们所期望的完备性关系为:
1=∣Ω⟩⟨Ω∣+λ∑∫(2π)3d3p2Ep(λ)1∣λp⟩⟨λp∣
我们接下来假设 x0>y0,并且丢掉不感兴趣的常数项 ⟨Ω∣ϕ(x)∣Ω⟩⟨Ω∣ϕ(y)∣Ω⟩ (这一项通常为零)。由此,两点关联函数成为:
⟨Ω∣ϕ(x)ϕ(y)∣Ω⟩=λ∑∫(2π)3d3p2Ep(λ)1⟨Ω∣ϕ(x)∣λp⟩⟨λp∣ϕ(y)∣Ω⟩(1)
我们可以如下处理矩阵元:
⟨Ω∣ϕ(x)∣λp⟩=⟨Ω∣eiP⋅xϕ(0)e−iP⋅x∣λp⟩=⟨Ω∣ϕ(0)∣λp⟩e−ip⋅x∣p0=Ep=⟨Ω∣ϕ(0)∣λ0⟩e−ip⋅x∣p0=Ep
最后一步运用了,ϕ(0) 与 Ω 在 boost 下的不变性。
将上述结果代入,再引入对 p0 的积分,(1) 式成为:
⟨Ω∣ϕ(x)ϕ(y)∣Ω⟩=λ∑∫(2π)4d4pp2−mλ2+iϵie−ip⋅(x−y)∣⟨Ω∣ϕ(0)∣λ0⟩∣2=∫0∞2πdM2ρ(M2)DF(x−y;M2)(2)
上式子第二行给出两点关联函数的 Kallen-Lehmann spectral representation。其中:
ρ(M2)=λ∑(2π)δ(M2−mλ2)∣⟨Ω∣ϕ(0)∣λ0⟩∣2(3)
称为 谱密度函数 spectral density function。
对于自由场的情形,不难得到:
ρ(M2)=2πδ(M2−m2)
即自由场中两点关联函数只会得到质量为 m 的基态,而不会产生多粒子激发态。
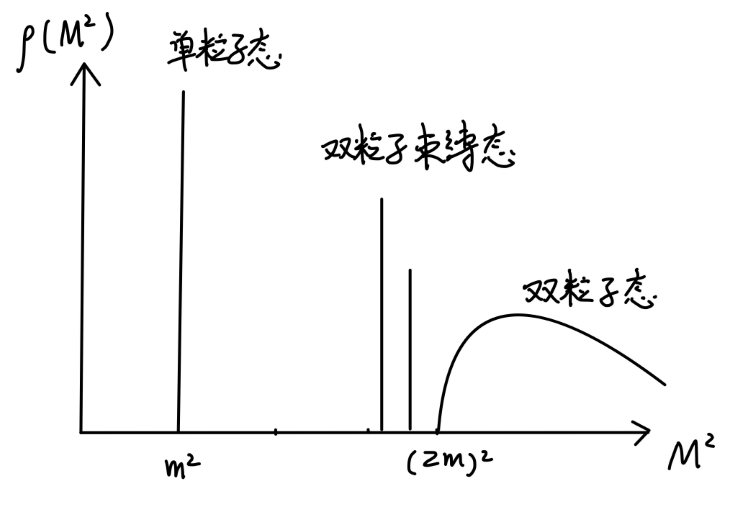
一个典型的谱密度有如下形式:
ρ(M2)=2πδ(M2−m2)⋅Z+(nothing else until M2≳(2m)2)
其中 Z 称为 场强重整化 field-strength renomalization。其中的质量 m 就是静止粒子对应的哈密顿量本征值,是粒子的物理质量(这将与我们之后讨论的:在拉格朗日量中出现的 裸质量 m0 相区分)。如何理解这个谱密度呢?首先,谱密度中出现的 δ 函数对应于传播子的 极点,这表现为分立谱,例如质量为 m 的单粒子态。在 M2≲(2m)2 时,两个粒子间由于存在相互作用,是可以产生一些束缚态的。在 M2≳(2m)2 时,产生多粒子态,这对应于传播子的 branch cut。
那么两点关联函数成为:
∫d4xeip⋅x⟨Ω∣Tϕ(x)ϕ(0)∣Ω⟩=∫0∞2πdM2ρ(M2)p2−M2+iϵi=p2−m2+iϵiZ+∫∼4m2∞2πdM2ρ(M2)p2−M2+iϵi(4)
比较真空两点关联函数:
⟨0∣Tϕ(x)ϕ(0)∣0⟩=p2−m2+iϵi
比较发现:一般的两点关联函数中包含场强重整化,且包含多粒子态的贡献。
对于 Dirac 场的两点关联函数。其具有以下结构
∫d4xeip⋅x⟨Ω∣Tψ(x)ψˉ(0)∣Ω⟩=p2−m2+iϵiZ2∑sus(p)uˉs(p)+⋯=p2−m2+iϵiZ2(p+m)+⋯
其中 Z2 是产生或湮灭一个单粒子态的概率:
⟨Ω∣ψ(0)∣p,s⟩=Z2us(p)
对应于 Dirac 场的场强重整化。
接下来我们来通过一个例子看看重整化的含义。
电子自能
根据微扰论,电子的两点关联函数 ⟨Ω∣Tψ(x)ψˉ(y)∣Ω⟩ 等价于如下费曼图的总和:

第一项对应于自由场的传播子:
p2−m02+iϵip+m0
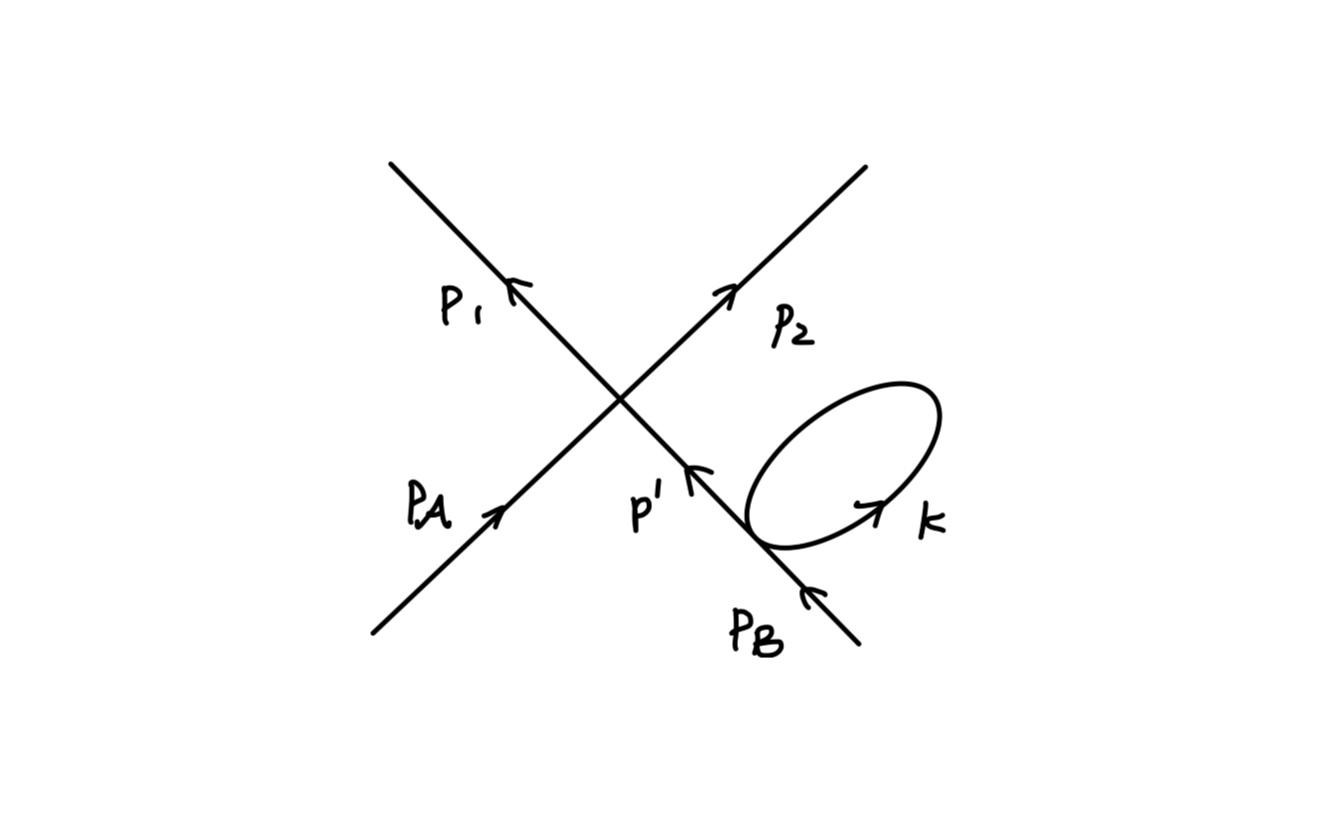
对于第二个费曼图,我们称为 电子自能图,根据费曼规则,其值为:
p2−m02i(p+m0)[−iΣ2(p)]p2−m02i(p+m0)
其中:
−iΣ2(p)=(−ie)2∫(2π)4d4kγμk2−m02+iϵi(k+m0)γμ(p−k)2−μ2+iϵ−i
这里 Σ2 指的是 e 的二阶项(含有 e2)对 Σ 的贡献,其中我们为光子引入了一个小质量 μ。通过费曼参数化,将上述积分中两个分母进行合并,即:
k2−m02+iϵ1k2−μ2+iϵ1=∫01dx[k2−2xk⋅p+xp2−xμ2−(1−x)m02+iϵ]21
如此可以得到:
−iΣ2(p)=−e2∫01dx∫(2π)4d4l(l2−Δ+iϵ)−2xp+4m0
其中:
l≡k−xpΔ=−x(1−x)p2+xμ2+(1−x)m02
为了解决紫外发散,我们使用 Pauli-Villars 正规化:
(k−p)2−μ2+iϵ1→(p−k)2−μ2+iϵ1−(p−k)2−Λ2+iϵ1
紧接着做 wick rotation,计算对 d4l 的积分,得到:
Σ2=2πα∫01dx(2m0−xp)log((1−x)m02+xμ2−x(1−x)p2xΛ2)(5)
我们首先考虑分母的行为,令分母为零,得到:
(1−x)m02+xμ2−x(1−x)p2=0
解得:
x=21+2p2m02−2p2μ2±2p21[p2−(m0+μ)2][p2−(m0−μ)2]
当 p2⩾(m0+μ)2 时,我们得到两个解 x∈[0,1]。此时是存在 branch cut 的。这对应产生一个电子加一个光子的两粒子态。
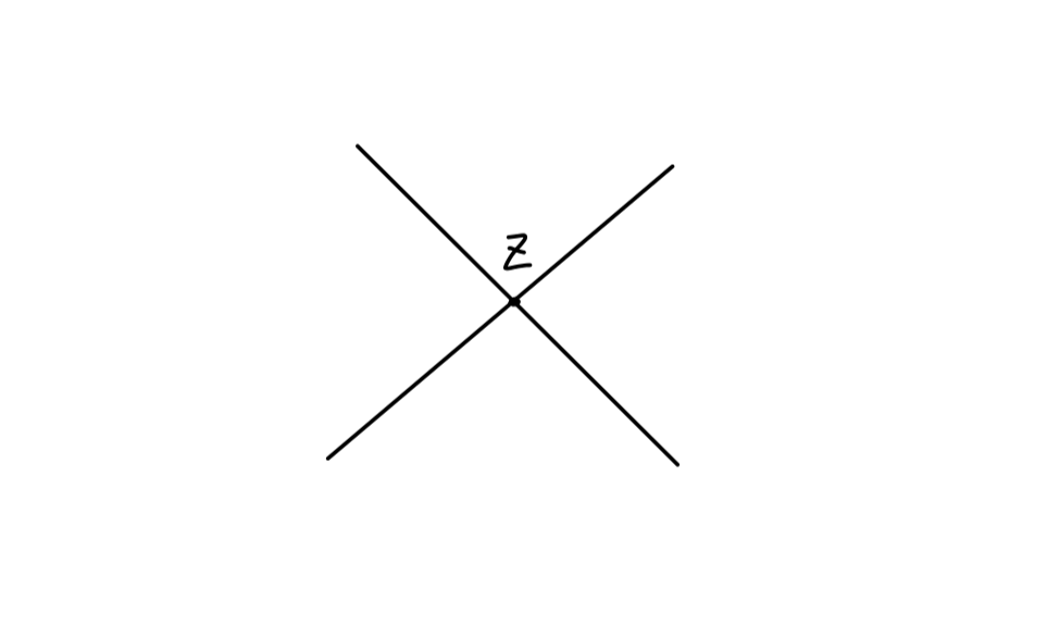
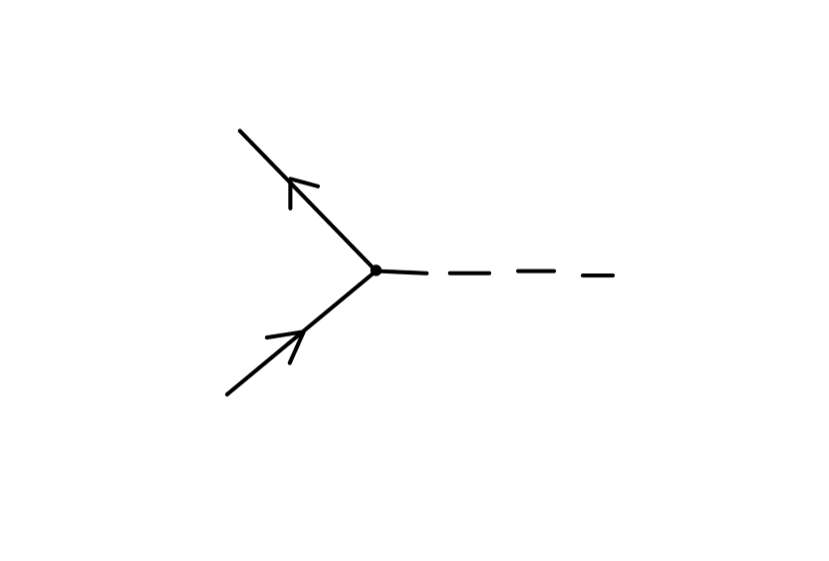
下面,我们定义 不可约单粒子图 one-particle irreducible(1PI):它们是那些“不能够通过去掉单个的连线成为两个图”的图。
例如:
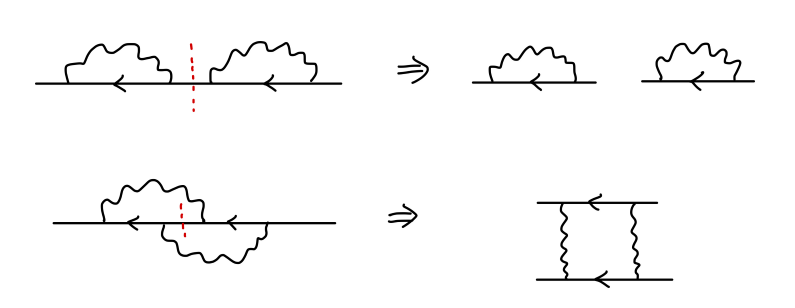
其中上面的图为可约图,下面的图为不可约图。
我们令 −iΣ(p) 代表所有具有两个外部费米子线的 1PI 图的值。
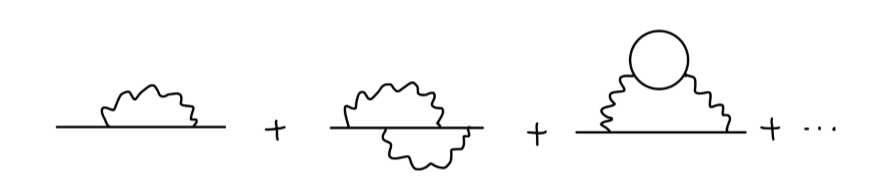
我们将 1PI 图表示为:
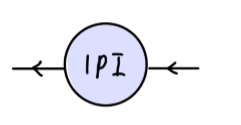
那么关联函数实际上是多个 1PI 图的总和:
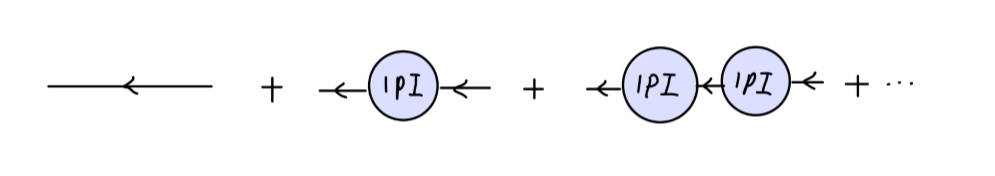
即:
∫d4x⟨Ω∣Tψ(x)ψˉ(0)∣Ω⟩eip⋅x=p2−m02i(p+m0)+p2−m02i(p+m0)(−iΣ)p2−m02i(p+m0)+⋯=p−m0i+p−m0i(p−m0Σ(p))+p−m0i(p−m0Σ(p))2+⋯=p−m0−Σ(p)i(6)
考虑上式极点对应于物理质量 m,即:
[p−m0−Σ(p)]∣p=m=0(7)
在极点附近,上述分母可以展开为:
(p−m)⋅(1−dpdΣ∣p=m)+O((p−m)2)
由此得到:
Z2−1=1−dpdΣ∣p=m(8)
由此,质量修正为:
δm=m−m0=Σ2(p=m)≈Σ2(p=m0)
那么代入公式 (5) 得到:
δm=2παm0∫01dx(2−x)log((1−x)2m02+xμ2xΛ2)Λ→∞→4π3αm0log(m02Λ2)(9)
那么如何解释 (9) 式中出现的 δm→∞ 呢?首先我们要说明:我们不可能测得电子得裸质量,电子一定是与电磁场耦合在一起的。我们测量得到的,当然是考虑电子自能后的物理质量 m。当 m0=0 时,ψL 与 ψR 是解耦的,同电磁场耦合不会产生质量项。因此质量修正 δm 将于 m0 成正比。即使质量修正出现无穷大的项,这并不影响我们的计算。在考虑 α 阶修正时,我们只需要将本来的裸质量 m0 替换成物理质量 m 即可。
得到对 Z2 的修正为:
δZ2=Z2−1=dpdΣ2∣p=m=2πα∫01dx[−xlog(1−x)2m2+xμ2xΛ2+2(2−x)(1−x)2m2+xμ2x(1−x)m2]
考虑我们之前得到对 δF1(0) 的修正:
δF1(0)=2πα∫01dxdydzδ(x+y+z−1)×[log((1−z)2m2+zμ2zΛ2)+(1−z)2m2+zμ2(1−4z+z2)m2]=2πα∫01dz(1−z)(log((1−z)2m2+zμ2zΛ2)+(1−z)2m2+zμ2(1−4z+z2)m2)
通过分部积分可以计算下列表达式:
∫01dz(1−2z)log((1−z)2m2+zμ2Λ2)=−∫01dzz(1−z)(1−z)2m2+zμ22(1−z)m2−μ2=∫01dz[(1−z)−(1−z)2m2+zμ2(1−z)(1−z2)m2]
因此得到:
δF1(0)+δZ2=2πα∫01dz[(1−2z)log(1−z)2m2+zμ2Λ2+(1−2z)logz+2(2−z)(1−z)2m2+zμ2z(1−z)m2+(1−z)2m2+zμ2(1−4z+z2)m2]=2πα∫01dz[(1−z)−(1−z)2m2+zμ2(1−z)(1−z2)m2]+(1−2z)logz+2(2−z)(1−z)2m2+zμ2z(1−z)m2+(1−z)2m2+zμ2(1−4z+z2)m2]=2πα∫01dz(1−z+(1−2z)logz)=2πα(z−z2)logz∣01=0
即:
δF1(0)+δZ2=0(10)
在这里,我们解决了一个疑问。在上一篇中,对形状因子的顶点修正是发散的,因此我们使用了 δF1(q2)−δF1(0) 来代替 δF1(0) 以保证 F1(q2) 在 q2=0 的取值为 1。那么现在考虑场强重整化后,对一个跃迁矩阵元的修正成为:
γμ→γμF1(q2)Z2≈γμ(1+δF1(q2)+δZ2)=γμ(1+δF1(q2)−δF1(0))
这正是我们在上一篇中的做法。